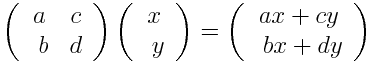# 2.1.1 css 相关知识

本质上就是数学中的矩阵计算

# 1.transform 的 rotate translateX 先后顺序有何不同

属性书写的先后顺序不同，也会造成最终的表现形式不同
结论就是写在后面的先执行

第一会改变中心点，第二会改变坐标系，所以请遵循先后顺序。

translateX等虽然让元素发生了位移，但是是不会改变元素的中心点

transform-origin 区别于景深，它是作用于变换的dom上
rotate scale skew 其实是围绕transform-origin指定的位置进行转换的，
之所以看起来是围绕中心点，是因为center是这个css的默认值而已

# matrix

matrix 其实是可以代替：偏移量（translate）,缩放（scale），斜切（skew），旋转（rotate）， 四大功能的，
任意一个matrix样式改变而来的形状也都能通过以上四个功能实现，它们是互通的。

假定matrix的六个参数用字母表示如下：transform: matrix(a,b,c,d,e,f);

• e和f 代表着偏移量translate，x和y轴

• a和d 代表着缩放比例scale,x 和y轴

• b和c 代表着斜切skew（具体参数和角度关系为, b-->tanθ y轴 c-->tanθ x轴 ,我们具体操作的时候还是要使用小数的）

• abcd 中的ad代表缩放(scale),bc代表者斜切(skew); abcd四个参数代表着旋转，这你可能难以理解，请继续往下看。

为啥6个数能做到，translate，scale，skew，rotate了，因为一个对应两个参数， 原来最后一个rotate 被缩放和斜切给替代了

• 对应的矩阵

a  c   e
b  d   f
0  0   1

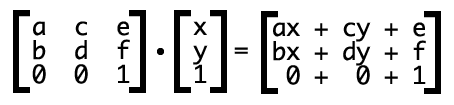
旋转是可以理解为, 旋转=规律的缩放+规律的斜切 这里的意思是旋转可以用缩放和斜切一起用来得到, 两者联系在于这个角度θ。具体如下：

matrix(cosθ,sinθ,-sinθ,cosθ,0,0)

# 矩阵运算

• 矩阵与矩阵的乘法:
  • 1、运算规则 　　A与B的乘积是这样一个矩阵：
    　　(1) 行数与（左矩阵）A相同，列数与（右矩阵）B相同，即．
    　　(2) C的第i行第j列的元素由A的第i行元素与B的第i列元素对应相乘，再取乘积之和．

第一个矩阵中第一行的数据分别与第二个矩阵中每一列的数据相乘后相加

a d g        i          a*i +d*m +g*n
b e h   *    m     =    b*i +e*m +h*n
c f j        n          c*i + f*m +j*n

# 2.transform动画和直接使用left、top改变位置有什么优缺点

通过调用translate，会启动硬件加速，即在GPU层对该元素进行渲染。
这样，CPU就会相对解放出来进行其他的计算，GPU对样式的计算相对较快，且保证较大的帧率。我们可以通过2d和3d的transform来启用GPU计算。

1，尽量使用keyframes和transform进行动画，这样浏览器会自身分配每帧的长度，并作出优化

2，如果非要使用js来进行动画，使用requestAnimateFrame

3，使用2d transform而不是改变top/left的值，这样会有更短的repaint时间和更圆滑的动画效果

4，移动端的动画效果可能会比pc端的差，因此一定要注意性能优化，尽量减少动画元素的DOM复杂性，待动画结束后异步执行DOM操作

• 参考：尽量使用translate而不是改变top/left进行动画（翻译）

# 参考

• transform
• understanding-the-css-transforms-matrix
• 如何优雅的使用css3的矩阵变换matrix(矩阵)
• 理解CSS3 transform中的Matrix(矩阵)
• 6.5 矩阵的运算及其运算规则